本文共 9981 字,大约阅读时间需要 33 分钟。
ä¸ã数组
(一)数组的优缺点:
优点:1:数组通过下标访问元素的效率很高。指定下标n的元素的地址:首地址+n*元素类型字节数。
2:数组可以保存若干个元素的值。
缺点:1:数组的长度是不能更改的。
2:数组进行元素的删除和插入操作的时候,效率比较低。需要移动大量的元素。
3:数组元素的类型只能是一种。
4:数组通过内容查找元素的效率是比较低的。
5:数组的元素是连续分配的,那么必须在堆内存中找到连续的指定内存空间才能容纳数组的所有的数据。对内存要求稍微多一些。
6:数组没有提供任何的封装,所有对元素的操作,都是通过自定义方法来实现的。对数组元素的操作比较麻烦。
java 提供了一整套的用于管理对象的容器。集合框架 collection framework。可以有效解决这些缺点。
(二)java.util.Arrays 工具类
jdk 提供了一个工具类:专门用于处理数组的工具类。
//一定记得导入 Arrays。
import java.util.Arrays;
public class Arrays extends Object
此类包含用来操作数组(比如排序和搜索)的各种方法
常用方法:
static int binarySearch(byte[] a, byte key)
使用二分搜索法来搜索指定的 byte 型数组,以获得指定的值。
static int binarySearch(byte[] a, int fromIndex, int toIndex, byte key)
使用二分搜索法来搜索指定的 byte 型数组的范围,以获得指定的值。
static boolean[] copyOf(boolean[] original, int newLength)
复制指定的数组,截取或用 false 填充(如有必要),以使副本具有指定的长度。
static void sort(byte[] a)
对指定的 byte 型数组按数字升序进行排序。
static String toString(boolean[] a)
返回指定数组内容的字符串表示形式。
static void arraycopy(Object src, int srcPos, Object dest, int destPos, int length)
从指定源数组中复制一个数组,复制从指定的位置开始,到目标数组的指定位置结束。
(三)main方法传递参数(了解):
main 方法的 字符串数组 参数的作用:
可以用来接收 控制台 在解释执行的时候,输入的一系列的 字符串 内容。 多个字符串对象可以使用空格分隔 输入即可。
public class TestString{
public static void main(String[] args){
for(String str : args){
print(str);
}
String str = "";
String[] strs = {"123","123","123","123","123","123"};
}
public static void print(String str){
System.out.println(str);
}
}
(å)Â 变参
变参方法:在jdk1.5 之后提供的功能。
语法:参数列表(接收的数据的类型 ... 变量名)
例子 (boolean ... values)
变参参数的特点:
1:变参参数可以接收的参数的数量[0-N]
2: 如果有定参的方法,有变参的方法,那么优先匹配定参的方法。
3:一个方法最多只能有一个变参参数,而且必须在参数列表的末尾。
4:方法在处理变参参数的时候,就当数组来处理即可。底层使用数组实现的。
5:变参参数既可以接收 数据类型若干个实参的值,还可以接收一个该类型的数组。
例:
需求:使用变参实现:写一个方法,可以接收任意个int类型的参数,将这若干个数据中的最大值返回。
//变参方法
public class TestChangeArgs{
public static void main(String[] args){
System.out.println(max());
System.out.println(max(1));
System.out.println(max(2,5));
System.out.println(max(3,4,8));
System.out.println(max(2,5,67,89));
System.out.println(max(32,54,67,7,56,45,34));
int[] arr = {45,34,32,54,76};
System.out.println(max(arr));
}
public static int max(int a, int b){
System.out.println("2个参数的方法");
return a > b ? a : b;
}
public static int max(int a, int b ,int c){
System.out.println("3个参数的方法");
return a > b ? (a > c ? a : c) : (b > c ? b : c);
}
//如果有方法可以接收参数的数量是任意个[0--n]?
public static int max(int ... values){
System.out.println("变参参数的方法");
if(values == null)return -1;
if(values.length == 0)return -2;
int max = values[0];
for(int i = 1;i< values.length;i++){
if(values[i] > max){
max = values[i];
}
}
return max;
}
public static void test(int a, int ... values){
}
}
ï¼äºï¼多维数组
一维数组:int[] values = new int[10];
二维数组:本质上还是一维数组
int[] array;
int[][] array;
初始化的方式:
动态的:int[][] array = new int[7][9];//代表了这个数组是一个7个元素的一维数组,每个一维数组的元素又是一个一维数组,最终的一维数组的元素的个数是9个。
其他样式:int[][] arr = new int[1][1];
int[] arr[] = new int[1][2];
int [][]arr = new int[2][3];
int arr[][] = new int[2][5];
静态方式:int[][] array1 = new int[][]{
{1,34,5,65,89},
{1,34,5},
{1,65},
{1,34,5,65,5,4,43,23}
};
int[][] array1 = {
{1,34,5,65,89},
{1,34,5},
{1,65},
{1,34,5,65,5,4,43,23}
};
//多维数组
import java.util.Arrays;
public class TestArray6{
public static void main(String[] args){
//高纬 代表的是有几个一维数组,低纬的数值代表的是每一个一维数组的元素的个数。
int[] array[] = new int[3][];
System.out.println(Arrays.toString(array));
//可以将每个一维数组的长度控制的不同。单独进行空间的分配。
array[0] = new int[3];
array[1] = new int[6];
array[2] = new int[1];
System.out.println(Arrays.toString(array));
System.out.println(array.length);//3
System.out.println(array[1].length);//6
int[][] array1 = new int[][]{
{1,34,5,65,89},
{1,34,5},
{1,65},
{1,34,5,65,5,4,43,23}
};
System.out.println(array1.length);//4
System.out.println(array1[2].length);//2
}
}
多维数组内存图:
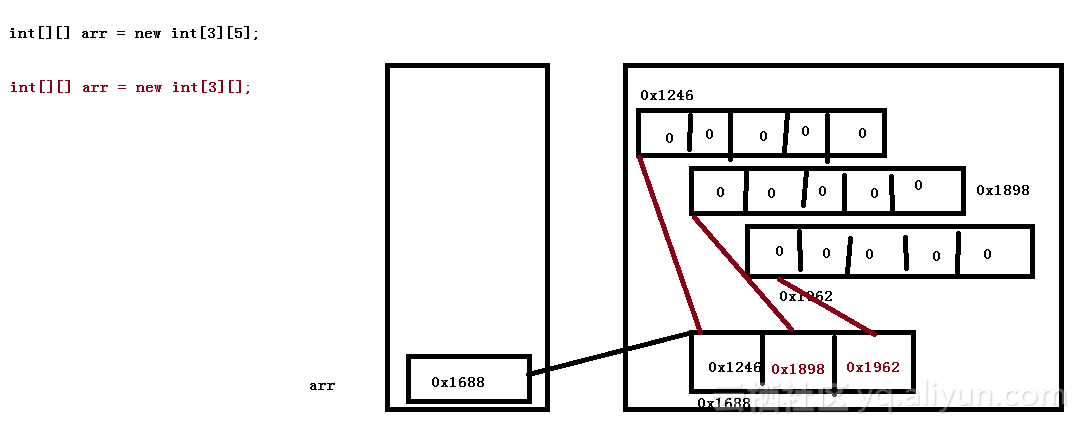
例1:
//使用二维数组中的元素,存储九九乘法表的结果,最后在将结果打印 实现九九乘法表的效果。
public static void test(){
//先对二维数组进行高纬空间的分配。
final int LEN = 9;
int[][] nine = new int[9][];
//然后在对每个一维数组进行单独的空间的分配。
for(int i=0;i<LEN;i++){
nine[i] = new int[i+1];
}
//在使用for 循环 将结果打印。
for(int i=1;i<=LEN;i++){
for(int j=1;j<=i;j++){
//使用数组元素保存
nine[i-1][j-1] = j * i;
System.out.print(j+"*"+i+"="+nine[i-1][j-1]+"; ");
}
System.out.println();
}
}
例2:偏算法,可以了解了解
//螺旋数组
public class TestArray11{
public static void main(String[] args){
int count = 6;
int[][] ints = test(count);
for (int i = 0; i < count; i++) {
for (int j = 0; j < count; j++) {
System.out.print(ints[i][j] + "\t");
}
System.out.println();
}
}
private static int[][] test(int count){
int[][] ints = new int[count][count];
final int RIGHT = 0;
final int DOWN = 1;
final int LEFT = 2;
final int UP = 3;
int dir = RIGHT;
int curRow = 0;
int curCol = 0;
for (int i = 1; i <= count * count; i++) {
switch(dir){
case RIGHT:
if(curCol < count){
if(ints[curRow][curCol] == 0){
ints[curRow][curCol] = i;
curCol ++;
}else{
curCol --;
dir = DOWN;
if(ints[curRow + 1][curCol] != 0){
return ints;
}else{
curRow ++;
ints[curRow][curCol] = i;
curRow ++;
}
}
}else{
curCol --;
dir = DOWN;
if(ints[curRow + 1][curCol] != 0){
return ints;
}else{
curRow ++;
ints[curRow][curCol] = i;
curRow ++;
}
}
break;
case DOWN:
if(curRow < count){
if(ints[curRow][curCol] == 0){
ints[curRow][curCol] = i;
curRow ++;
}else{
curRow --;
dir = LEFT;
if(ints[curRow][curCol-1] != 0){
return ints;
}else{
curCol --;
ints[curRow][curCol] = i;
curCol --;
}
}
}else{
curRow --;
dir = LEFT;
if(ints[curRow][curCol-1] != 0){
return ints;
}else{
curCol --;
ints[curRow][curCol] = i;
curCol --;
}
}
break;
case LEFT:
if(curCol >=0){
if(ints[curRow][curCol] == 0){
ints[curRow][curCol] = i;
curCol --;
}else{
dir = UP;
curCol ++;
if(ints[curRow - 1][curCol] != 0){
return ints;
}else{
ints[--curRow][curCol] = i;
curRow --;
}
}
}else{
curCol ++;
dir = UP;
if(ints[curRow - 1][curCol] != 0){
return ints;
}else{
ints[--curRow][curCol] = i;
curRow --;
}
}
break;
case UP:
if(curRow >=0){
if(ints[curRow][curCol] == 0){
ints[curRow][curCol] = i;
curRow --;
}else{
dir = RIGHT;
curRow++;
if(ints[curRow][curCol+1] != 0){
return ints;
}else{
ints[curRow][++curCol] = i;
++curCol;
}
}
}else{
curRow ++;
dir = RIGHT;
if(ints[curRow][curCol+1] != 0){
return ints;
}else{
ints[curRow][++curCol] = i;
++curCol;
}
}
break;
}
}
return ints;
}
}
äºã递归
概念:递归调用:方法直接或者间接的调用自身的过程。
void a(int n){
//a(n-1);
b(n-1);
}
void b(int n){
a(n-1);
}
什么样的问题可以使用递归调用来解决?
1:一个问题可以被分解为若干个子问题。
2:子问题的解决方案和问题的解决方案一致。
3:最终问题的解决依赖于子问题的解决。
例1:
//求 n 的阶乘。
n!:n*(n-1)*(n-2)*...2*1;
1:一个问题可以被分解为若干个子问题。
2:子问题的解决方案和问题的解决方案一致。
3:最终问题的解决依赖于子问题的解决。
5! = 5 * 4 !
4! = 4 * 3!
3! = 3 * 2!
2! = 2 * 1!
1! = 1;
//求n 的阶乘 时间复杂度 T(n) = O(n); 空间复杂度 S(n) = O(n)
public static int fac(int n){
int result = 0;
if(n == 1){
result = 1;
}else{
result = n * fac(n-1);
}
return result;
}
例2:
//斐波那契数列 前两个数都是1,从第三个数开始,是前两个数之和
//1,1,2,3,5,8,13。。。。 T(n) = O(n);
//求第n 个位置上的斐波那契数列的值
public static int febo(int n){
if(n == 1 || n == 2){
return 1;
}else{
return febo(n-1) + febo(n-2);
}
}
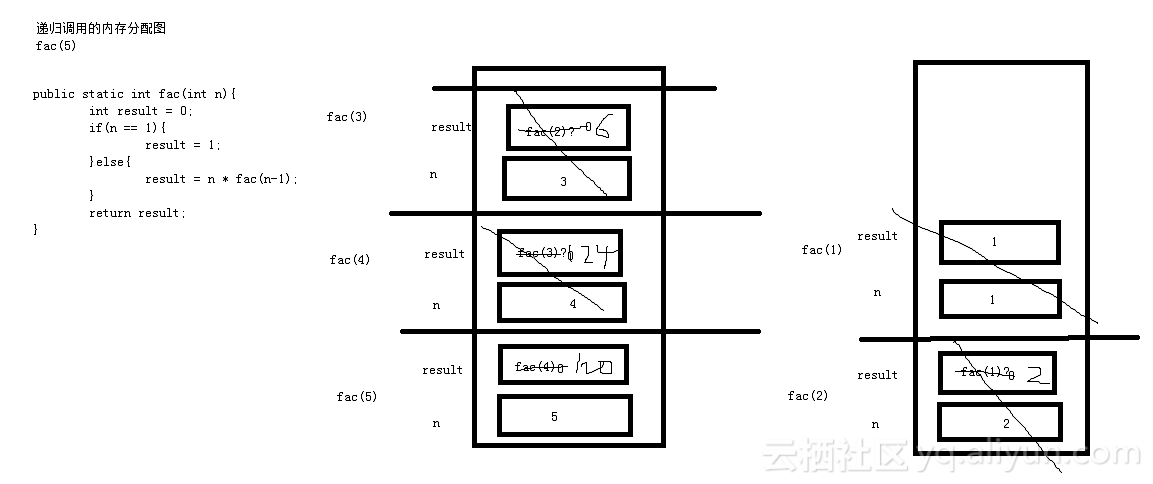
递归调用的优缺点:
优点:代码简单,思路比较简单。
缺点:对栈内存的消耗比较大,如果控制不好,那么就会造成 栈内存溢出。
递归调用的过程中,必须在某些情况下存在自己不调用自己的情况。以保证程序可以在合适的时候正确返回。
三、算法(algorithm )(了解)
是指令的集合,是为解决特定问题而规定的一系列操作。
简单的说,算法就是计算机解题的过程。
举例:如何求0+1+2+3+...10000=?
算法1:依次相加 while do-while for
算法2:高斯解法:首尾相加*50 (1+10000)*10000/2 100*101/2
算法3:使用递归实现: sum(100) = sum(99)+100 sum(99)= sum(98)+99 ..... sum(2) = sum(1)+2 sum(1) = 1
评价算法优劣的依据:复杂度(时间复杂度和空间复杂度)
时间复杂度是指执行算法所需要的计算工作量
空间复杂度是指执行这个算法所需要的内存空间
(一)时间复杂度(Time Complexity))定义
时间频度:
一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。
但我们不可能也没有必要对每个算法都上机测试。
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度,表示为T(n),n表示问题的规模
时间复杂度
但有时我们想知道它变化时呈现什么规律,想知道问题的规模,而不是具体的次数,此时引入时间复杂度。
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,
若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。
记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
T(n)=O(f(n))
或者说:时间复杂度就是时间频度去掉低阶项和首项常数。
注意:时间频度与时间复杂度是不同的,时间频度不同但时间复杂度可能相同。
比如:某两个算法的时间频度是 T(n) = 100000n2+10n+6 T(n) = 10n2+10n+6 T(n) = n2
但是时间复杂度都是 T(n) = O(n2)
总结:随着n 的增大,如果两个频度的函数的结果是无限接近的,那么这两个算法的时间复杂度是相同的。
时间复杂度考量的是算法的变化的趋势。
最坏时间复杂度和平均时间复杂度
最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明,讨论的时间复杂度均是最坏情况下的时间复杂度。
这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界,这就保证了算法的运行时间不会比任何更长。
在最坏情况下的时间复杂度为T(n)=O(n),它表示对于任何输入实例,该算法的运行时间不可能大于O(n)。
平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,算法的期望运行时间。鉴于平均复杂度
第一,难计算
第二,有很多算法的平均情况和最差情况的复杂度是一样的。
所以一般讨论最坏时间复杂度
比如 我要求你在字典里查同一个字,告诉我这个字在字典的那一页。
如果一页一页的翻,你需要多少时间呢?
最优的情况就是这个字在第一页,
最坏的情况就是这个字是 整本字典的最后一个字。
所以即使我故意为难你,你也不会花费比找整本字典最后一个字还长的时间。
当然,此时聪明的你就会想用部首、笔画等去查,才不要傻乎乎的一页一页翻,
此时的你就会择优选择,因为此时你最坏得情况就是我给你部首笔画最多、除部首外笔画最多的一个超级复杂的一个字,但显然比翻整本字典快得多。
为了进一步说明算法的时间复杂度,我们定义 Ο、Ω、Θ符号。
Ο(欧米可荣)符号给出了算法时间复杂度的上界(最坏情况 <=),比如T(n) =O(n2)
Ω(欧米伽)符号给出了时间复杂度的下界(最好情况 >=),比如T(n) =Ω(n2)
而Θ(西塔)给出了算法时间复杂度的精确阶(最好和最坏是同一个阶 =),比如T(n) =Θ(n2)
时间复杂度计算
根本没有必要计算时间频度,即使计算处理还要忽略常量、低次幂和最高次幂的系数,所以可以采用如下简单方法:
⑴ 找出算法中的基本语句;
算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。
⑵ 计算基本语句的执行次数的数量级;
只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,
可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。
⑶ 用大Ο记号表示算法的时间性能。
将基本语句执行次数的数量级放入大Ο记号中。
总结:先找出基本的执行单元的语句。然后算出语句的执行的频度,去掉低阶项,常数项,去掉最高阶的系数。
T(n) = O(f(n));
T(n) = O(n^2)
时间复杂度举例
一个简单语句的时间复杂度为O(1)。
int count=0;
100个简单语句的时间复杂度也为O(1)。(100是常数,不是趋向无穷大的n)
int count=0;
如果一个算法随着问题规模的增大,执行的基本语句的次数都是一个定值,那么时间复杂度 都是 O(1)
T(n) = O(1);
一个循环的时间复杂度为O(n)。
int n=8, count=0;
for (int i=1; i<=n; i++)
count++;
T(n)=O(n)
时间复杂度为O(log2 n)的循环语句。
int n=8, count=0;
for (int i=1; i<=n; i*=2)
count++;
n=2 2
n=4 3
n=8 4
n=16 5
230=1024*1024*1024 = 1000*1000*1000=10亿
时间复杂度为O(n2)的二重循环。
int n=8, count=0;
for (int i=1; i<=100n; i++)
for (int j=1; j<=10n; j++)
count++;
时间复杂度为O(nlog2n)的二重循环。
int n=8, count=0;
for (int i=1; i<=n; i*=2)
for (int j=1; j<=n; j++)
count++;
时间复杂度为O(n2)的二重循环。
int n=8, count=0;
for (int i=1; i<=n; i++)
for (int j=1; j<=i; j++)
count++;
1+2+3+4....+n=(1+n)*n/2
需要复杂些数学运算:1+2+3+.....+n=(n+1)*n/2 时间复杂度是 O(n2)
后面讲解查找和排序算法时会大量的设计时间复杂度,作为选择查找和排序算法的重要依据
常用的时间复杂度级别
常数阶O(1)
对数阶O(log2n)
线性阶O(n)
线性对数阶O(n*log2n)
平方阶O(n2)
立方阶O(n3)
...
k次方阶O(nk)
指数阶O(2n)
阶乘阶O(n!)
上面各种时间复杂度级别,执行效率越来越低。
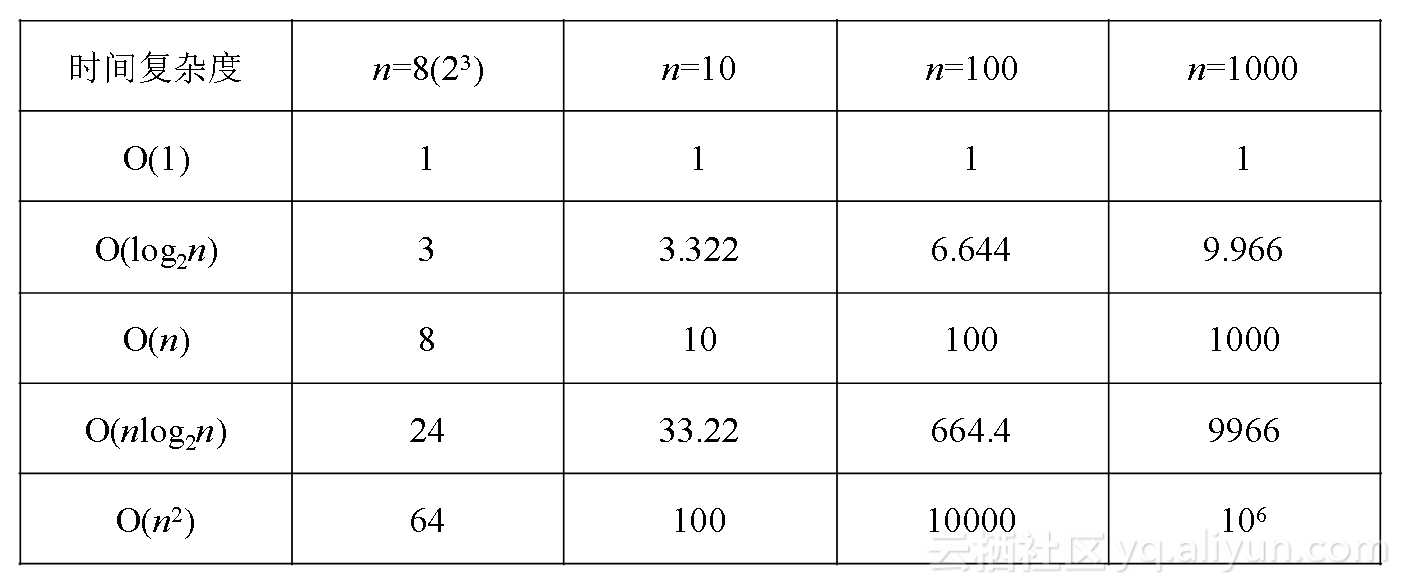
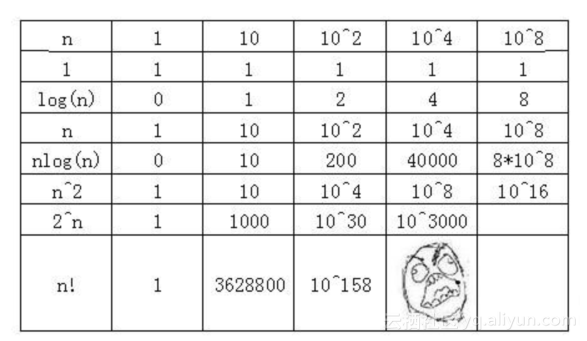
大家发现对数阶O(log2n)和线性阶O(n)的效率差异了吗,当n=10的8次方(1亿)时,执行此时一个是1亿次,一个是8次。
所以编写算法时一定要注意时间复杂度的选择。
空间复杂度计算:
表示方法
S(n) = O(f(n));
固定的变量的个数
S(n) = O(1);
例://1-n的累加和。
n 就是问题的规模。
1:使用while 循环 sum +=i
T(n) = n;
T(n) = O(n).
2:高斯算法 (1+n)*n/2
T(n) = 1;
T(n) = O(1);

转载地址:http://mbouo.baihongyu.com/